Je reviens sur ma table traçante qui me sert – pour rappel – de démonstrateur quand à ma capacité à piloter précisément les pattes de mon robot. Il m’aura fallu un peu de temps pour prendre en main le matériel du fablab, m’outiller, concevoir et réaliser ce que je présente dans cet article (et accessoirement commencer un nouveau boulot en parallèle).
1. La patte
1.1. Double U
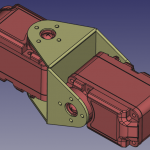
Pour refaire la pièce de jonction, entre les servomoteurs 0 et 1, que j’appelle “double U”, j’ai repris exactement la même conception qu’initialement. J’ai commencé par dessiner en 3D mon assemblage avec freeCAD (cf. illustrations plus bas). Pour faciliter le pliage de l’aluminium, j’ai opté pour la solution proposée sur ce forum : faire des rainures en V (à 90°) au niveau des pliures. Cela présente l’inconvénient d’être moins résistant qu’un pliage classique mais l’avantage d’obtenir un rendu plus propre avec des moyens limités.
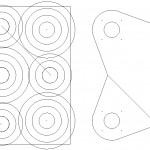
Cette méthode implique de faire des rainures sur les deux faces dans le cas de cette pièce. Pour retourner la pièce sans perdre le repère de la CNC, j’ai dû passer par la fabrication une pièce intermédiaire qui permet de reprendre la pièce fabriquée sur ses alésages ∅ 8 mm (réalisés par fraisage). J’ai dessiné en 2D sous freeCAD, puis repris avec libreCAD pour les finitions (les trous de perçage sont remplacés par des points), afin d’obtenir un fichier DXF exploitable avec l’outil dxf2gcode (cf. illustrations). Rappel : j’utilise une configuration personnalisée de dxf2gcode pour générer du gcode exploitable par la CNC du fablab.
- Perçage avec un forêt ∅ 2 mm.
- Alésages ∅ 4 et 8 mm avec une fraise ∅ 4 mm, puis reprise des fixations sur ces alésages pour maintenir les pièces après détourage.
- Surfaçage de la pièce intermédiaire et détourage des deux pièces avec une fraise ∅ 4 mm.
- Rainurage sur la face 1 avec un foret à pointer ∅ 5 mm, puis retourner la pièce sur la pièce intermédiaire.
- Rainurage sur la face 2 avec un foret à pointer ∅ 5 mm.
Après pliage on obtient une pièce nettement mieux finie que la première version (faite sans CNC : découpages à la scie et pliages à l’étau), des côtes plus précises et des parallélismes et perpendicularités plus exactes.
Les fichiers (freecad, dxf, iso) pré-cités sont téléchargeables ici : doubleU_files.
1.2. Porte stylo
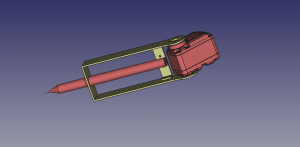
J’ai reconçu complètement le porte stylo avec freeCAD afin d’assurer des côtes plus précises, et qui soient répétables en cas de démontage/remontage ce qui n’était pas le cas de la première version. Le résultat de cette conception est représenté ci-dessous.
Il est composé de deux pièces. Une principale, se fixant sur le servomoteur et permettant de glisser le stylo dans son orifice. Le petit décrochage du stylo, au niveau du bouchon, vient en butée contre la pièce pour assurer le positionnement précis et reproductible du stylo. La seconde pièce permet de rigidifier le première, de maintenir l’écartement du côté du servomoteur et aussi de maintenir l’autre extrémité du stylo en position.
Ces deux pièces sont pliées en utilisant un rainurage à 90° comme pour le double U. J’ai dessiné ces pièces en 2D sous freeCAD, repris avec libreCAD et généré le fichier ISO avec dxf2gcode (cf. illustrations).
- Pointage et rainurage avec le foret à pointer ∅ 5 mm.
- Perçage avec un forêt ∅ 2 mm.
- Alésages avec une fraise ∅ 4 mm, puis reprise des fixations sur ces alésages pour maintenir la pièce après détourage.
- Détourage avec une fraise ∅ 4 mm.
- Pointage et rainurage avec le foret à pointer ∅ 5 mm.
- Perçage avec un forêt ∅ 2 mm, puis reprise des fixations sur ces perçages pour maintenir la pièce après détourage.
- Détourage avec une fraise ∅ 4 mm.
Après pliage et assemblage on obtient une pièce nettement mieux finie que la première version – qui était un assemblage de pièces standards – et des côtes plus précises. Je connais maintenant la côte entre l’axe de rotation du servomoteur et le bout du stylo (Y4 dans le modèle) : 145 mm.
Les fichiers (freecad, dxf, iso) pré-cités sont téléchargeables ici : PenSupport_files.
2. La maquette
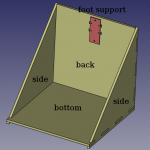
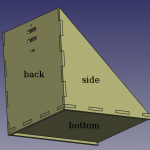
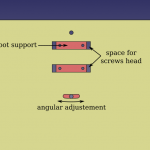
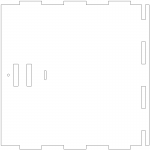
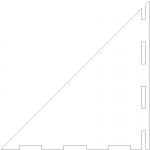
J’avais des problèmes de rigidité et de perpendicularité sur ma première maquette. J’ai réalisé la conception suivante (cf. illustrations) avec du contreplaqué de 5 mm d’épaisseur découpé par laser au Fablab. Aussi, j’ai ajouté le réglage de la position angulaire – suivant l’axe horizontal – du support de patte (en rouge ci-dessous). Ce dernier est en aluminium et usiné à la CNC.
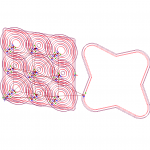
Pour faciliter la lecture en position, j’ai dessiné avec inkscape un quadrillage dont le pas est de 5 mm. Les lignes rouges sont les références des axes (zéros), les vertes ont des pas de 50 mm. J’ai imprimé et collé ces quadrillages sur toutes les surfaces. Le résultat final de la maquette est photographié ci-dessous.
Les fichiers (freecad, dxf, iso) pré-cités sont télécharges ici : setup_files.
3. Première amélioration
- servomoteur 0, zero0 = – 1,3°
- servomoteur 1, zéro1 = – 2,6°
- servomoteur 2, zéro2 = -2,6°
- X0 = 0 mm
- Y0 = 39,8 mm
- Z0 = 162,4 mm
- Y1 = 30,5 mm
- Y2 = 43,5 mm
- Y3 =145 mm
“S’il vous plaît… dessine-moi un mouton !”
Heu… on va commencer par plus simple 🙄
3.1. Dessine-moi un trait
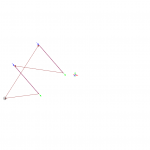
J’ai écrit le code testLeg-move-line pour tracer un trait depuis la coordonnée (X, Y, Z) = (50 mm, 120 mm, 0 mm) jusqu’à (-50 mm, 120 mm, 0 mm), qui donne le résultat sur la vidéo.
Vous aurez remarqué que le stylo ne touche pas la surface. J’ai donc répété la trajectoire avec une coordonnée en Z = -1.5 mm pour palier à ce problème.
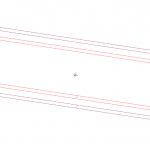
Le trait ainsi obtenu (cf. photo) est décalé de 5 mm de celui attendu (Y = 125 mm au lieu de Y = 120 mm). On observe de plus des variations d’environs 2 mm autour d’une trajectoire réellement rectiligne. Il mesure 102 mm de long au lieux de 100 mm. Ce résultat présente tout de même une nette amélioration en terme de rectitude et de dimension par rapport à la première version de maquette.
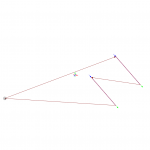
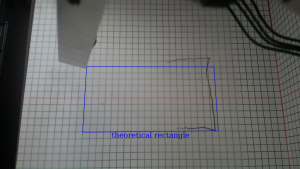
3.2. Dessine-moi un rectangle
- (25 mm, 150 mm, 0 mm)
- (-25 mm, 150 mm, 0 mm)
- (-25 mm, 50 mm, 0 mm)
- (25, 50 mm, 0 mm)
- (25 mm, 150 mm, 0 mm)
Je n’ai volontairement pas introduit le décalage de Z=-1,5 mm ce qui permet d’observer que ce n’est pas un décalage constant mais qu’il varie en fonction de la position sur Y.
La conclusion c’est que je ne suis pas encore prêt à dessiner un mouton… Et vous serez d’accord avec moi, où est le meilleurs endroit pour apprendre à le faire ? L’école pardi !
4. De retour à l’école
Pour parvenir à mon but, je vais essayer d’affiner la valeur de mes 9 constantes par une méthode d’apprentissage qui se décompose en 2 étapes : collecter des données expérimentales d’apprentissage, puis optimiser les constantes à partir du modèle théorique pour que le résultat soit au plus proche des données d’apprentissage.
4.1. Données d’apprentissage
Pour collecter les données j’ai écrit ce code permettant aussi bien de déplacer les servomoteurs manuellement – pour un positionnement rapide mais grossier – qu’en les pilotant – pour un positionnement plus fin. J’ai obtenu cet échantillon (tableau libre office) pour lequel je me suis contenté de données pour lesquelles Z = 0.
4.2. Optimisation des constantes
Pour faire tourner mon optimisation, j’ai réutilisé la fonction kinematics_direct_model() que j’avais écrite précédemment. Pour évaluer la capacité d’une solution (ensemble de valeurs des 9 constantes) à s’approcher des résultats expérimentaux de l’apprentissage, j’ai écrit la fonction eval_solution() ci-dessous.
function objectives = eval_solution(variables)
exec('./kinematics_direct_model.sci',-1);
// pre-processing
X0 = variables(1);
Y0 = variables(2);
Z0 = variables(3);
Y1 = variables(4);
Y2 = variables(5);
Y3 = variables(6);
zerotheta1 = variables(7);
zerotheta2 = variables(8);
zerotheta3 = variables(9);
learnedData = [-26.70, -46.60, 22.10,50,150,0
-1.60, -51.10, 14.00,0,165,0
15.90, -45.60, 23.10,-35,155,0
39.10, -55.00, 7.80,-80,135,0
29.90, -27.30, 64.80,-35,100,0
-0.30, -28.00, 68.10,0,100,0
-22.10, -28.60, 57.70,30,120,0
-58.60, -33.50, 46.60,85,95,0
-45.90, -28.60, 69.10,40,80,0
23.40, -35.50, 72.30,-10,65,0
65.20, -29.30, 56.00,-80,75,0
89.30, -28.30, 59.60,-80,40,0
-7.10, -62.20, 59.60,0,20,0
-76.60, -29.60, 67.80,55,55,0
-74.00, -29.60, 57.70,80,65,0];
nbData = size(learnedData,1);
errors = zeros(1,nbData);
// evaluation of errors
for data = 1:nbData
[X, Y, Z] = kinematics_direct_model(X0, Y0, Z0, Y1, Y2, Y3, (-zerotheta1+learnedData(data,1))*%pi/180, (-zerotheta2+learnedData(data,2))*%pi/180, -(-zerotheta3+learnedData(data,3))*%pi/180);
// distance between measured and computed positions
errors(data) = sqrt((X - learnedData(data,4))^2 + (Y - learnedData(data,5))^2 + (Z - learnedData(data,6))^2);
// for initial tests and debug only
mprintf('Error%i : dX=%f dY=%f dZ=%f \n',data, (X - learnedData(data,4)), (Y - learnedData(data,5)), (Z - learnedData(data,6)));
end
objectives = [max(errors), mean(errors)];
endfunction
Voici le résultat de cette fonction pour les valeurs des constantes utilisées plus haut :
-->exec('./eval_solution.sce', -1)
-->variables = [0, 39.8, 162.4, 30.5, 43.5, 145, -1.3, -2.6, -2.6];
-->objectives = eval_solution(variables);
Error1 : dX=-0.902922 dY=-6.801795 dZ=-2.912867
Error2 : dX=0.630275 dY=-4.827485 dZ=-1.700956
Error3 : dX=0.997917 dY=-5.357017 dZ=-2.362157
Error4 : dX=0.073521 dY=-1.286704 dZ=-1.029974
Error5 : dX=1.480147 dY=-4.852143 dZ=-0.679835
Error6 : dX=-0.949180 dY=-5.821488 dZ=-0.437680
Error7 : dX=-1.962627 dY=-6.391095 dZ=-1.366910
Error8 : dX=-6.945211 dY=-5.089716 dZ=-2.779897
Error9 : dX=-4.773301 dY=-4.477978 dZ=-0.361709
Error10 : dX=0.515402 dY=-4.579004 dZ=0.713149
Error11 : dX=5.495528 dY=-2.804533 dZ=-1.657798
Error12 : dX=4.993925 dY=-0.985490 dZ=-1.366787
Error13 : dX=-2.414854 dY=-3.973790 dZ=1.646215
Error14 : dX=-6.072287 dY=-2.364055 dZ=-1.140905
Error15 : dX=-7.352996 dY=-2.572978 dZ=-2.187619
Si on regarde les erreurs sur X, Y et Z pour chacun des points d’apprentissage, on retrouve une erreur quasi-systématique sur Y d’environs 5 mm ainsi que sur Z d’environs 1.5 mm. Plus globalement, cette solution donne une erreur maximale de 9 mm et une erreur moyenne de 6 mm en positionnement. La fonction objectif (parfois aussi appelée fonction coût) ainsi définie permet d’utiliser directement un algorithme d’optimisation de type algorithme génétique. J’ai jeté mon dévolu sur le NSGA2 parce qu’il est disponible par défaut dans scilab, qu’il est reconnu et aussi parce qu’il gère les problèmes d’optimisation multiobjectifs (on peut donc minimiser l’erreur maximale et l’erreur moyenne).
Je me suis inspiré du tutoriel “Multiobjective Optimization and Genetic Algorithms” du site Openeering pour écrire le processus d’optimisation suivant :
clear
// load function in case it is not already done
exec('./eval_solution.sce',-1);
// research space
min_bound = [-10, 30, 150, 20, 35, 135, -10, -10, -10];
max_bound = [ 10, 50, 170, 40, 55, 155, 10, 10, 10];
// optimisation configuration
PopSize = 100;
Proba_cross = 0.5;
Proba_mut = 0.3;
NbGen = 500;
NbCouples = 110;
Log = %T;
nb_disp = 10;
pressure = 0.1;
ga_params = init_param();
ga_params = add_param(ga_params,'dimension',2);
ga_params = add_param(ga_params,'minbound',min_bound');
ga_params = add_param(ga_params,'maxbound',max_bound');
// Performing optimization
printf("Performing optimization:\n");
[pop_opt, fobj_pop_opt, pop_init, fobj_pop_init] = optim_nsga2(eval_solution, PopSize, NbGen, Proba_mut, Proba_cross, Log, ga_params);
// Compute Pareto front and filter
[f_pareto,pop_pareto] = pareto_filter(fobj_pop_opt,pop_opt);
// Optimal front function definition
f1_opt = linspace(0,1);
f2_opt = 1 - sqrt(f1_opt);
// Plot solution: Pareto front
scf(1);
// Plotting final population
plot(fobj_pop_opt(:,1),fobj_pop_opt(:,2),'g.');
// Plotting Pareto population
plot(f_pareto(:,1),f_pareto(:,2),'k.');
title("Pareto front (#NbGen="+string(NbGen)+")","fontsize",3);
xlabel("min the max","fontsize",4);
ylabel("min the mean","fontsize",4);
legend(['Final pop.','Pareto pop.']);
// Generate table of pareto front
nb_Pareto = size(pop_pareto);
table_Pareto = zeros(size(pop_pareto),11);
for i = 1:nb_Pareto
table_Pareto(i,1:9) = pop_pareto(i)';
table_Pareto(i,10:11) = f_pareto(i);
end
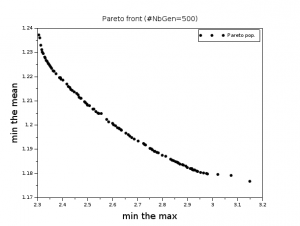
Son exécution m’a donné le front de Pareto ci-dessous dont les erreurs maximales varient entre 2,3 et 3,2 mm et les erreurs moyennes varient entre 1,17 mm et 1,24 mm.
- servomoteur 0, zero0 = – 2,1°
- servomoteur 1, zéro1 = – 1,7°
- servomoteur 2, zéro2 = -0,3°
- X0 = 1,8 mm
- Y0 = 40,6 mm
- Z0 = 165,3 mm
- Y1 = 29,9 mm
- Y2 = 46,5 mm
- Y3 =144,9 mm
Ces valeurs arrondies impactent peu le résultat : erreur maximale = 2,4 mm, une erreur moyenne = 1,2 mm.
4.3. Test de la solution optimale
J’ai reproduit les mêmes tests que précédemment, à commencer par le trait. Le code est le même, seules les valeurs des constantes ont été modifiées. Aucune compensation en Z n’est appliquée.
J’ai alors obtenu un tracé beaucoup plus précis comme le montre la photo suivante.
J’ai ensuite reproduit le test du rectangle en réutilisant le code du test initial aux valeurs des constantes près. Comme le montre la vidéo ci-desous, la force exercée par les servomoteur sur la pointe du stylo est telle qu’elle s’est tordue et que le servomoteur 2 s’est mis en défaut de surcharge… C’est pas très glorieux ! Deux origines à ce problème : 1) le stylo se déplace à “rebrousse poil” ce qui augmente le frottement ; 2) l’erreur du positionnement en Z entraîne une compensation par le couple allant jusqu’aux limites acceptables.
J’ai retenté ma chance sur le tracé d’un carré en prenant en compte une différence de niveau de 0,5 mm pour relâcher les efforts. J’ai donc écris ce code qui produit la vidéo ci-dessous.
Le résultat est alors plus probant comme le montre la photo suivante. On remarque sur la vidéo que les frottements du stylo “à rebrousse poil” sont encore importants. Mais cette fois on obtient une forme plus proche du résultat escompté.
5. What’s next?
Pour conclure, la reconception du dispositif expérimental ainsi que l’optimisation des constantes ont permis d’améliorer les capacités de la table traçante. J’aimerais tout de même aller plus loin et résoudre ces problèmes d’efforts qui dégradent le tracé, abiment le stylo et peuvent aller jusqu’à une mise en défaut des servomoteurs.
- Étudier s’il serait pertinent d’utiliser le tableau de valeurs angulaires (cf. p.55 du manuel) des servomoteurs plutôt que la notion de pas.
- Étudier si l’utilisation des courbes de saturation (cf. p.36 du manuel) pour des réponses élastiques des servomoteurs, voir même piloter dans la génération de trajectoire l’effort de la pointe du stylo en s’appuyant sur le modèle mécanique.
- Si les efforts dus aux frottements de la pointe du stylo “à rebrousse poil” sont trop importants, étudier l’ajout d’un quatrième servomoteur permettant de maintenir le stylo perpendiculaire à la surface.




































Pas mal tes avancés. Félicitations!
Je vois que tu maitrises de mieux en mieux la CNC, et du coup la découpe laser.