Les premières fois que j’ai lu le manuel des servomoteurs HerkuleX DRS-0101 et DRS-0201, je suis resté perplexe face à la grandeur désignée par PWM. S’agit-il d’un pulse width modulation (MLI en français) ? D’un couple moteur (car il est parfois décrit comme la charge) ? D’autre chose ?
C’est dans le but d’essayer d’élucider ce mystère que j’écris cet article en pratiquant de la rétro-ingénierie sur les servomoteurs. Et pour être honnête avec vous, à l’heure où j’écris ces premières lignes je n’ai pas de réponse précise (bien qu’une petite idée).
1 Modélisation
Vous l’aurez sans doute compris, j’aime bien m’appuyer sur les modèles théoriques pour comprendre ce qu’il se passe 💡 .
1.1 Modèle électromécanique du MCC
La documentation nous indique que pour les deux modèles de servomoteurs (DRS-0101 et DRS-0201), les moteurs utilisés sont à courant continue (MCC). J’utilise la modélisation proposée par wikipedia (somme toute classique) dont le schéma électrique idéalisé est ci-dessous.
Je synthétise ci-après les éléments qui m’intéressent de l’article de wikipedia en me plaçant dans le cas d’une excitation constante.
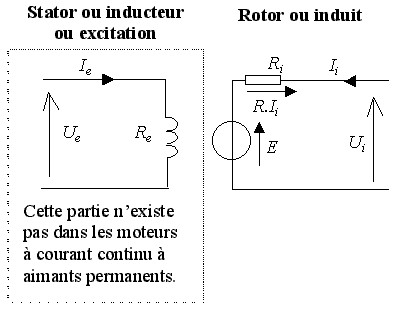 La loi des mailles nous donne la tension aux bornes de l’induit : Ui = E + Ri Ii. La loi de Lenz nous permet de déterminer la force contre-électromotrice : E = K Ω. La force de Laplace nous permet quand à elle de déterminer le couple électromécanique : Cm = K Ii. Dans ces différentes formules, les paramètres suivant interviennent :
La loi des mailles nous donne la tension aux bornes de l’induit : Ui = E + Ri Ii. La loi de Lenz nous permet de déterminer la force contre-électromotrice : E = K Ω. La force de Laplace nous permet quand à elle de déterminer le couple électromécanique : Cm = K Ii. Dans ces différentes formules, les paramètres suivant interviennent :- Ui : la tension d’entrée (en V)
- Ii : le courant d’entrée (en A)
- Ri : la résistance de l’induit (en Ω)
- K : la constante électromagnétique (en V.s/rad)
- Ω : la vitesse de rotation du moteur (en rad/s)
- Cm : le couple du moteur (en N.m)
En assemblant les trois équations, j’obtiens : Ui = K Ω + Cm Ri/K.
1.2 Commande du MCC
Cette dernière équation nous montre que lorsque le besoin en couple (Cm) est constant, alors la vitesse de rotation (Ω) dépend linéairement de la tension d’entrée (Ui). C’est la raison pour laquelle le pilotage du MCC se fait en général en faisant varier cette tension Ui. Un moyen simple et efficace de le faire lorsqu’on pilote le moteur avec un microcontrôleur est d’utiliser une sortie MLI (modulation de largeur d’impulsion) – PWM (pulse-width modulation) en anglais – reliée à l’électronique de puissance (pont en H par exemple, pour pouvoir aussi piloter le sens de rotation). La fonction de la MLI est de faire varier la tension d’entrée du moteur, mais comment ?
La sortie d’un microcontrôleur ne peut prendre que 2 états : GND (0 V) ou Vcc (en général 5V). L’électronique de puissance est alimentée avec une tension (Ua). La MLI va faire varier l’état de la sortie en créneaux avec un rapport cyclique (α) compris entre 0 et 1 – c’est-à-dire que la sortie est à Vcc pendant une durée α.p (p étant la période), puis à GND pendant (1 – α).p. Le filtrage naturel dû à l’inductance du moteur va lisser les créneaux. Le signal d’entrée du moteur sera donc “vu” comme une tension continue dont la valeur est la moyenne du signal en créneaux, soit Ui = α × Ua.
1.3 Modèle mécanique dynamique
- Cm le couple moteur appliqué sur son axe de rotation (en N.m),
- Cc le couple de la charge appliqué sur l’axe de rotation du moteur (en N.m),
- JO est le moment d’inertie de la charge par rapport l’axe de rotation du moteur (en kg.m2),
- dΩ/dt est l’accélération angulaire (en rad/s2).
Lorsqu’on est en régime établi (vitesse constante) on a alors dΩ/dt = 0, soit Cm = – Cc.
2 Hypothèse
Mon hypothèse est que la grandeur PWM dont la valeur varie entre 0 et 1023 correspond au rapport cyclique de la MLI, c’est-à-dire α = PWM/1023. Si c’est le cas, on peut alors écrire : Ua PWM/1023 = K Ω + Cm Ri/K (1).
Maintenant que les bases théoriques nécessaires sont posées, je vais présenter les essais expérimentaux en charge statique puis en rotation à vide, pour vérifier si cette hypothèse est valide. J’ai commencé par remettre le servomoteur à sa configuration d’usine.
#include <HkxSetup.h>
void setup() {
pinMode(13, OUTPUT);
digitalWrite(13, LOW);
// set current servo baudrate and the serial port
hkxBaudrate baudrate = HKX_666666;
HardwareSerial& serialPort = Serial1;
// set options for the factory reset
bool keepID = false; // true = ID is kept, false = ID reset
bool keepBaudrate = false; // true = baudrate is kept, false = baudrate reset
HkxPrint printout = HkxPrint(); // No printout
HkxCommunication communication = HkxCommunication(baudrate, serialPort, printout); // Communication with the servo on Serial1
HkxSetup setupServos(communication, printout); // setup the servos
setupServos.factoryResetAll(keepID, keepBaudrate);
digitalWrite(13, HIGH);
}
void loop() {
// put your main code here, to run repeatedly:
}
3 Charge statique
3.1 Dispositif expérimental
J’ai installé le servomoteur dans son dispositif expérimental (photos ci-dessous), qui va permettre d’appliquer une charge constante connue pour une position fixe du servomoteur. Cette charge est appliquée à l’aide d’un poids de 10 N – soit une masse de 1 kg – (bouteille d’eau – visiblement ressortie de la poubelle de trie vu son état 🙄 ) dont l’élégante ficelle relie son goulot à l’une des 12 encoches de la barre fixée au servomoteur. Les encoches sont espacées de 10 mm, la première étant positionnée à 20 mm du centre de rotation. Il est alors possible d’appliquer des couples de charge entre 0,2 N.m et 1,3 N.m avec un pas de 0,1 N.m. La barre est en carbone et ne pèse que 3 g, pas de quoi influencer la charge, mais elle doit être maintenue horizontale pour que la valeur du couple de charge soit correcte. Le servomoteur est alimenté – non plus par une batterie comme dans un article précédent mais – par une alimentation stabilisée à tension réglable.
- PWM : la grandeur que nous cherchons à identifier, retournée par le servomoteur.
- Ua : la tension d’alimentation du servomoteur, donnée par l’alimentation stabilisée et par le servomoteur (j’utiliserai la valeur de l’alimentation stabilisée).
- Cm : le couple appliqué au servomoteur, donné par l’encoche sur laquelle est positionné le poids.
Comme la vitesse angulaire est constante (étant nulle), le couple du moteur est égal au couple de la charge au signe près : Cm = – Cc (cf. paragraphe 1.3). J’ai écrit le code suivant – pour maintenir le servomoteur à sa position et afficher PWM et Ua à intervalles réguliers – avec lequel j’ai fait mes mesures.
#include <HkxSetup.h>
// global variables
byte ID = 253; // ID of the servo
HkxPrint* printoutLib;
HkxPrint* printoutCode;
HkxCommunication* communication;
HkxSetup* setupServos;
String message;
void setup() {
delay(2000); // wait 2 seconds to open the serial monitor
printoutLib = new HkxPrint(Serial, 9600); // Printout errors on the serial monitor
printoutCode = new HkxPrint(*printoutLib, true, true, true); // Printout errors on the serial monitor
communication = new HkxCommunication(HKX_115200, Serial1, *printoutLib); // Communication with the servo on Serial1
setupServos = new HkxSetup(*communication, *printoutLib); // setup the servos
setupServos->clearOneStatus(ID);
// modify the max voltage
setupServos->setAllTemperatureVoltage (8500, 6714, 13000);
// modify the control system
setupServos.setAllControlSystem (440, 8000, 0, 0, 0);
// place the servo in position
setupServos->setOneTorqueLEDControl(ID, HKX_TORQUE_FREE, HKX_LED_BLUE);
printoutCode->infoPrint("Please place the servo in horizontal position");
delay(5000);
setupServos->setOneTorqueLEDControl(ID, HKX_TORQUE_ON, HKX_LED_GREEN);
printoutCode->infoPrint("Start acquisition");
// Title for information display
message = ";\t mVolt \t;\t PWM";
printoutCode->infoPrint(message);
delay(1000);
}
void loop() {
uint16_t voltage;
uint16_t PWM;
// Get the behaviour
byte error = setupServos->getBehaviour(ID, &voltage, HKX_NO_VALUE, HKX_NO_VALUE, HKX_NO_VALUE, HKX_NO_VALUE, HKX_NO_VALUE, &PWM, HKX_NO_VALUE, HKX_NO_VALUE, HKX_NO_VALUE);
if(error == 0){
message = ";\t ";
message += voltage;
message += " \t;\t ";
message += PWM;
printoutCode->infoPrint(message);
} else if(error == 1){
printoutCode->errorPrint("Input not correct");
} else if(error == 2){
printoutCode->errorPrint("Servo not connected");
} else if(error == 3){
printoutCode->errorPrint("Data not consistent");
}
delay(1000); // refresh every second
}
3.2 Réponse PWM/couple
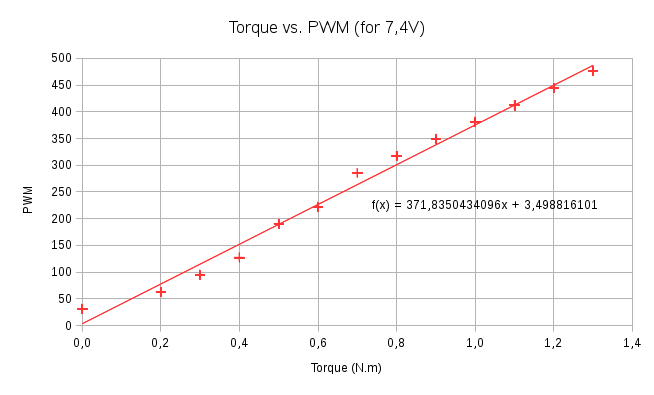
J’ai réalisé ces tests avec Ua = 7,4 V (tension optimale d’après le manuel). Vous pouvez voir sur la figure ci-dessous que la réponse obtenue est proportionnelle entre PWM et Cm, ce qui vérifie l’équation (2).
3.3 Réponse tension d’entrée / couple/PWM
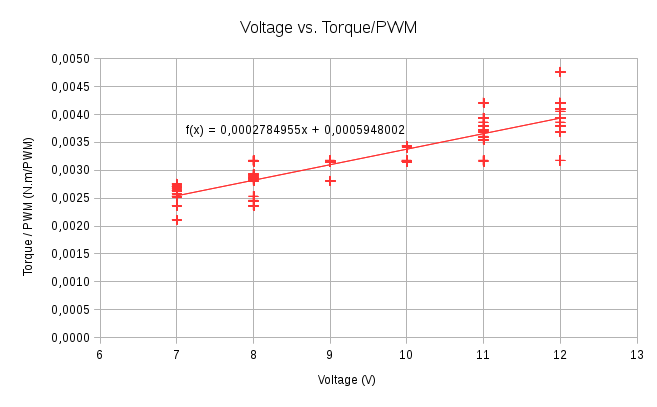
Ensuite, j’ai relevé les valeurs de PWM pour chaque couple possible, le tout avec Ua variant de 7 à 12 V (gammes de valeurs nominales) avec un pas de 1 V. Vous pouvez voir sur la figure ci-dessous que la réponse obtenue est proportionnelle entre Ua et Cm/PWM, ce qui vérifie une nouvelle fois l’équation (2).
4 Rotation à vide
4.1 Dispositif expérimental
Le test de rotation à vide est beaucoup plus simple à mener expérimentalement étant donné qu’il ne consiste qu’à faire tourner le servomoteur sans charge. J’ai donc repris le même dispositif auquel j’ai retiré la barre crantée.
- PWM : la grandeur que nous cherchons à identifier, elle sera la consigne du servomoteur pour effectuer une rotation continue.
- Ua : la tension d’alimentation du servomoteur, donnée par l’alimentation stabilisée et par le servomoteur (j’utiliserai la valeur de l’alimentation stabilisée).
- Ω : la vitesse angulaire du servomoteur, donnée par le servomoteur.
L’encodage du servomoteur n’est réalisé que sur 320° en rotation. Il existe donc une zone de 40° dans laquelle les valeurs de position et de vitesse sont fausses. J’ai “filtré” ces valeurs – qui sont identifiables visuellement – pour mes relevés.
J’ai écrit le code suivant – pour effectuer une rotation continue à partir d’une valeur PWM et retourner Ω et Ua à intervalles réguliers – avec lequel j’ai fait mes mesures.
#include <HkxSetup.h>
#include <HkxContRotation.h>
// global variables
byte ID = 253; // ID of the servo
HkxPrint* printoutLib;
HkxPrint* printoutCode;
HkxCommunication* communication;
HkxSetup* setupServos;
HkxContRotation* servo;
String message;
int16_t PWM;
void setup() {
delay(2000); // wait 2 seconds to open the serial monitor
printoutLib = new HkxPrint(Serial, 9600); // Printout errors on the serial monitor
printoutCode = new HkxPrint(*printoutLib, true, true, true); // Printout errors on the serial monitor
communication = new HkxCommunication(HKX_115200, Serial1, *printoutLib); // Communication with the servo on Serial1
setupServos = new HkxSetup(*communication, *printoutLib); // setup the servos
servo = new HkxContRotation(ID, *communication, *printoutLib); // drive continuous rotation
setupServos->clearOneStatus(ID);
// modify the control system
setupServos->setAllControlSystem (440, 8000, 0, 0, 0);
// Title for information display
message = ";\t mVolt \t;\t velocity";
printoutCode->infoPrint(message);
delay(1000);
PWM = 0;
}
void loop() {
servo->moveRotation(PWM, HKX_NO_VALUE, HKX_NO_VALUE);
uint16_t voltage;
int16_t velocity;
// Get the behaviour
byte error = servo->getBehaviour(&voltage, HKX_NO_VALUE, &velocity, HKX_NO_VALUE);
if(error == 0){
message = ";\t ";
message += voltage;
message += " \t;\t ";
message += velocity;
printoutCode->infoPrint(message);
} else if(error == 1){
printoutCode->errorPrint("Input not correct");
} else if(error == 2){
printoutCode->errorPrint("Servo not connected");
} else if(error == 3){
printoutCode->errorPrint("Data not consistent");
}
// if we get a valid byte, read analog ins:
if (Serial.available() > 0) {
String income = Serial.readString();
PWM = income.toInt();
printoutCode->infoPrint(String(PWM));
}
delay(1000); // refresh every second
}
4.2 Réponse PWM/vitesse
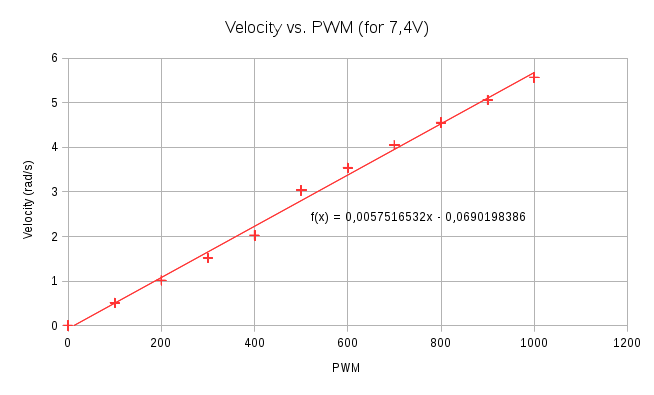
J’ai réalisé ces tests avec Ua = 7,4 V (tension optimale d’après le manuel). Vous pouvez voir sur la figure ci-dessous que la réponse obtenue est proportionnelle entre PWM et Ω, ce qui vérifie l’équation (3).
4.3 Réponse tension d’entrée / vitesse/PWM
Ensuite, j’ai relevé Ω pour PWM variant de 0 à 1000 avec un pas de 100, le tout pour Ua variant de 7 à 12 V avec un pas de 1 V. Vous pouvez voir sur la figure ci-dessous que la réponse obtenue est proportionnelle entre la Ua et Ω/PWM, ce qui vérifie une nouvelle fois l’équation (3).
5 Vérification de l’hypothèse
Les résultats expérimentaux montrent, malgré une dispersion non négligeable dans les données, que la modélisation adoptée décrit correctement le comportement du servomoteur et confirme mon hypothèse (cf. paragraphe 2), à savoir, la grandeur PWM correspond bien au rapport cyclique (α) de la MLI.
Je me dit que maintenant que j’ai toutes ces jolies équations, il serait dommage de ne pas essayer d’aller plus loin ! Pourquoi ne pas essayer d’estimer le couple moteur ?
6 Estimation du couple
Précédemment, j’ai vérifié que la réponse du système correspondait bien à la modélisation proposée. Maintenant il s’agit de donner des valeurs aux différentes constantes et d’évaluer la capacité de ce modèle à estimer le couple moteur. Ces résultats ne sont valables que pour le modèle DRS-0101, n’ayant pas de DRS-0201 sous la main.
6.1 Évaluation des constantes
Je cherche ici à déterminer la valeur des constantes de l’équation (1) (pour rappel : Ua PWM/1023 = K Ω + Cm Ri/K). Au paragraphe 3.3, je me suis placé dans le cas d’une charge statique, c’est-à-dire : Ua PWM/1023 = T Ri/K. J’ai mis en forme les données précédemment collectées dans le graphique ci-dessous représentant Cm en fonction de Ua.PWM. La régression linéaire donne la valeur de Ri/K = 2,8186450832.
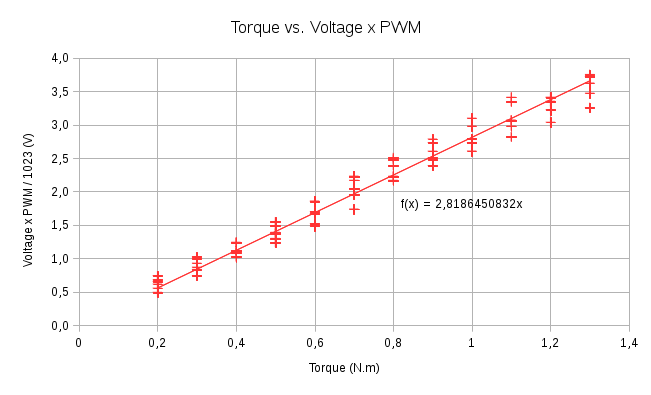 Au paragraphe 4.3, je me suis placé dans le cas d’une rotation à vide, c’est-à-dire : Ua PWM/1023 = K Ω. J’ai mis en forme les données précédemment collectées dans le graphique ci-dessous représentant Ω en fonction de Ua.PWM. La régression linéaire donne la valeur de K = 1,2759099269.
Au paragraphe 4.3, je me suis placé dans le cas d’une rotation à vide, c’est-à-dire : Ua PWM/1023 = K Ω. J’ai mis en forme les données précédemment collectées dans le graphique ci-dessous représentant Ω en fonction de Ua.PWM. La régression linéaire donne la valeur de K = 1,2759099269.
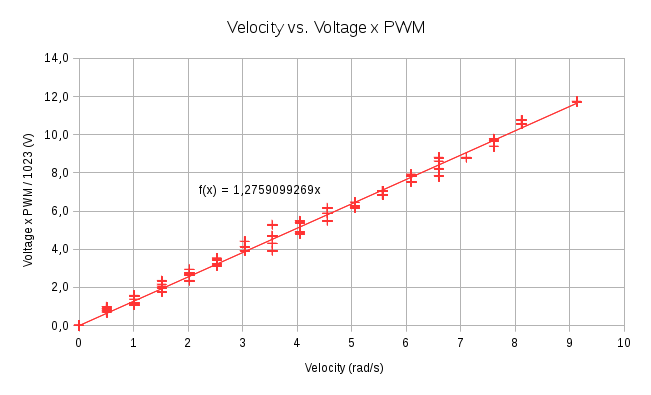 On obtient comme modèle électromécanique : Ua PWM/1023 = 1,2759099269 Ω + 2,8186450832 Cm (4).
On obtient comme modèle électromécanique : Ua PWM/1023 = 1,2759099269 Ω + 2,8186450832 Cm (4).
6.2 Quand l’asservissement s’en mêle
Lors de premiers tests que j’avais menés antérieurement, je me suis rendu compte qu’en fonction des paramètres de l’asservissement, les résultats obtenus sont différents. Je profite donc de cette étude pour vérifier l’influence de ces paramètres sur le rapport Ua.PWM/Cm. D’après la documentation, l’asservissement est composé d’un régulateur PID avec un feedforward à deux gains.
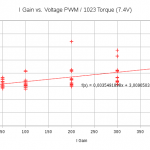
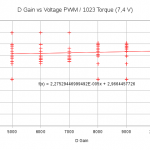
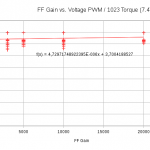
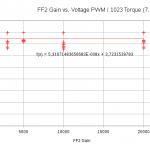
Vous remarquerez sur les courbes ci-dessous que les gains proportionnel (P) et intégral (I) ont une réponse linaire, alors que les autres paramètres (D, FF et FF2) semblent ne pas avoir avoir d’influence dans le cas d’une charge statique. Notez que pour chacun des graphiques les paramètres non-étudiés de l’asservissement sont à leur valeur par défaut (D = 440, I = 0, D = 8000, FF = 0, FF2 = 0) sauf pour l’étude de FF2 pour laquelle FF = 1000. Comme le pilotage en rotation continue du servomoteur ne fait pas intervenir l’asservissement étant donné qu’on pilote directement la PWM. L’asservissement n’a donc pas d’influence sur la vitesse dans le cas précédemment étudié de la rotation à vide.
Je ne peux donc que vous recommander de réévaluer les constantes K et Ri/K dès que vous modifiez l’asservissement si vous voulez estimer la valeur du couple moteur. Ci-après je poursuit mes tests avec les valeurs par défaut des paramètres de l’asservissement.
6.3 Estimation du couple moteur
Pour tester mes paramètres, je me suis placé dans une configuration pour laquelle et couple (Cm) et la vitesse (Ω) interviennent, mais où la composante dynamique n’intervient pas. J’ai donc repris le même dispositif expérimental que pour la charge statique (paragraphe 4.1), pour lequel je vais appliquer un mouvement à vitesse constante à la barre. Étant donné que je ne peux pas appliquer un mouvement de rotation continue, j’ai configuré les phases d’accélération et de décélération pour qu’elles soient les plus courtes possibles.
J’ai écrit le code suivant – pour effectuer une course de 40° dans les deux sens (vers le haut puis vers le bas) et retourner les valeurs moyennes de PWM, Ua et Ω – avec lequel j’ai fait mes mesures. Deux zones de 5° en début et fin de trajectoire ne sont pas prises en compte pour éviter les zones d’accélération et de décélération.
#include <HkxPosControl.h>
#include <HkxSetup.h>
void setup() {
delay(2000); // wait 2 seconds to open the serial monitor
// Inputs
byte ID = 253; // ID of the servo
uint16_t moveTime = 2000; // time for the moves
int16_t minAngle = 00;
int16_t maxAngle = 400;
int16_t angleMargin = 50;
// variables
String message;
uint16_t voltage;
int16_t velocity,PWM,positionAngle;
float averageVoltage, averageVelocity, averagePWM;
HkxPrint printoutLib = HkxPrint(Serial, 9600); // Printout errors on the serial monitor
HkxPrint printoutCode = HkxPrint(printoutLib, true, true, true); // Printout errors on the serial monitor
HkxCommunication communication = HkxCommunication(HKX_115200, Serial1, printoutLib); // Communication with the servo on Serial1
HkxPosControl servo = HkxPosControl(ID, communication, printoutLib); // drive continuous rotation
// Set high acceleration
HkxSetup setupServos = HkxSetup(communication, printoutLib);
setupServos.setAllAcceleration(0, 0);
servo.clearStatus();
// Title for information display
printoutCode.infoPrint("mVolt \t PWM \t vel");
// move to initial position
servo.movePosition(minAngle, 1, HKX_LED_PINK, false);
delay(1000);
for(int i=0 ; i<2 ; i++){
int16_t startP = i==0?minAngle:maxAngle; //start move
int16_t stopP = i==0?maxAngle:minAngle; //stop move
int16_t startA = startP + (stopP-startP>0?1:-1)*angleMargin; //stard acquisition
int16_t stopA = stopP + (stopP-startP>0?-1:1)*angleMargin; //stop acquisition
int count = 0;
averageVoltage = 0;
averageVelocity = 0;
averagePWM = 0;
servo.movePosition(stopP, moveTime, HKX_LED_BLUE, false);
long timerInit = millis();
while (!servo.isInPosition() && millis()-timerInit < moveTime+500){
byte error = servo.getBehaviour(&voltage, HKX_NO_VALUE, &positionAngle, &velocity, &PWM, HKX_NO_VALUE, HKX_NO_VALUE, HKX_NO_VALUE);
if(error == 0){
if(stopP-startP>0?(positionAngle > startA && positionAngle < stopA):(positionAngle < startA && positionAngle > stopA)){
averageVoltage += voltage;
averageVelocity += velocity;
averagePWM += PWM;
count++;
}
} else if(error == 1){
printoutCode.errorPrint("Input not correct");
} else if(error == 2){
printoutCode.errorPrint("Servo not connected");
} else if(error == 3){
printoutCode.errorPrint("Data not consistent");
}
}
averageVoltage /= count;
averageVelocity /= count;
averagePWM /= count;
message = String(averageVoltage);
message += " \t ";
message += averagePWM;
message += " \t ";
message += averageVelocity;
printoutCode.infoPrint(message);
delay(1000);
}
}
void loop() {
}
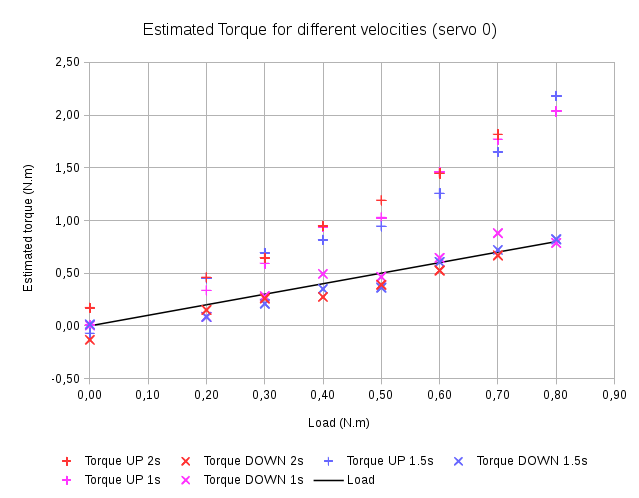
J’ai relevé les valeurs moyennes de PWM, Ua et Ω en faisant varier la charge puis j’ai estimé le couple moteur à partir de l’équation (4) du paragraphe 6.1. J’ai représenté les résultats obtenus sur le graphique ci-dessous pour différentes valeurs du temps en mouvement (donc de la vitesse). La vidéo ci-dessous montre une acquisition pour 0,5 N.m avec des déplacements de 2 secondes. Au delà de 0,7 N.m de charge pour le mouvement de 2 secondes, et de 0,8 N.m de charge pour les mouvements de 1 et 1,5 secondes, le servomoteur décroche à la monté – c’est-à-dire qu’il rentre en mode surcharge.
Vous remarquerez d’abord que la vitesse du déplacement n’influence pas le résultat, par contre le couple moteur est différent à la montée et à la descente. À la descente, les résultats sont très proches de la charge. L’erreur est inférieure à 0,15 N.m ce qui est similaire à la dispersion observée au paragraphe 6.1. À la monté par contre, le couple est très supérieur à la charge, d’un facteur d’environ 2,3.
J’explique cette différence par la présence de frottement dans les engrenages, effet que j’avais négligé dans l’équation dynamique (paragraphe 1.3). Lorsque le couple de charge (Cc) est opposé à la vitesse de rotation (montée) alors le couple de frottement (Cf) des engrenages s’oppose à la rotation, donc s’ajouter à la charge. Inversement, lorsque le couple de charge (Cc) est dans le même sens que la vitesse de rotation (descente) alors le couple de frottement (Cf) des engrenages s’oppose à la rotation et s’ajouter au moteur (Cm), comme l’illustre la figure ci-dessous.
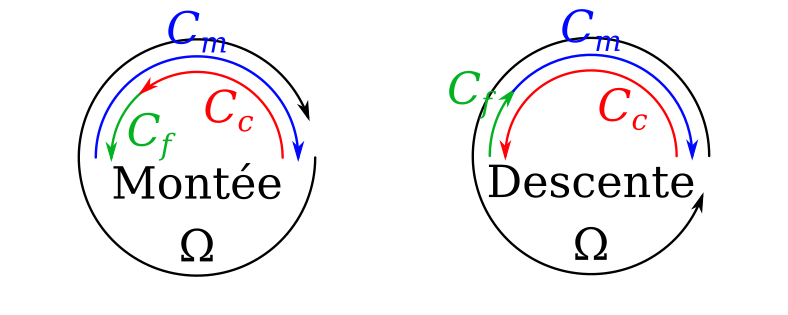 Me direz-vous, dans ce cas, si le couple est double à la monté, il devrait être de moitier à la descente – alors qu’on remarque qu’elle est quasiment égale à la charge (à peine inférieure). Pour l’expliquer, il faut regarder dans les entrailles du servomoteur qui est composé d’un moteur et d’un réducteur (engrenages). Ce dernier permet, en appliquant une vitesse rapide et un couple faible à l’entrée (côté moteur), d’obtenir une vitesse lente et un couple élevé en sortie (côté palonnier). Cela étant dit, on comprend qu’un tel frottement a beaucoup plus d’impact quand il s’oppose au moteur – alors que son couple avant l’engrenage est faible – que lorsqu’il s’oppose à la charge – où le couple produit par le moteur après l’engrenage est nettement plus important.
Me direz-vous, dans ce cas, si le couple est double à la monté, il devrait être de moitier à la descente – alors qu’on remarque qu’elle est quasiment égale à la charge (à peine inférieure). Pour l’expliquer, il faut regarder dans les entrailles du servomoteur qui est composé d’un moteur et d’un réducteur (engrenages). Ce dernier permet, en appliquant une vitesse rapide et un couple faible à l’entrée (côté moteur), d’obtenir une vitesse lente et un couple élevé en sortie (côté palonnier). Cela étant dit, on comprend qu’un tel frottement a beaucoup plus d’impact quand il s’oppose au moteur – alors que son couple avant l’engrenage est faible – que lorsqu’il s’oppose à la charge – où le couple produit par le moteur après l’engrenage est nettement plus important.
J’ai donc validé la valeur de mes constantes et suis capable d’estimer la valeur du couple moteur. Il est nécessaire de moyenner les valeurs sur une période de temps car les micro-régulations du servomoteur induisent des erreurs locales conséquentes. Par contre, j’introduis un nouveau terme dans mon équation dynamique qui devient : Cm + Cc + Cf = JO × dΩ/dt.
- Cf = 1,269 × Cc, si signe(Cc) = signe(Ω)
- Cf = – 0,125 × Cc, si signe(Cc) ≠ signe(Ω)
6.4 Reproductibilité des résultats
Les résulats que nous venons d’obtenir sont-ils reproductibles sur d’autres servomoteurs de la même gamme (DRS-0101) oubien faut-il refaire le calcul des constantes pour chacun d’entre eux ?
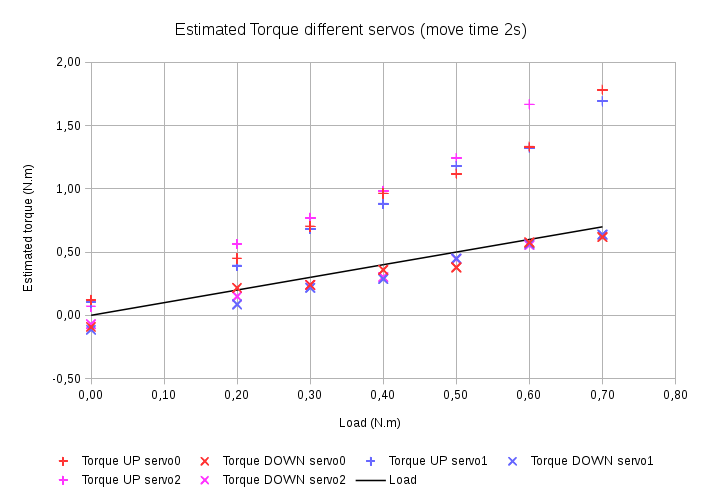
J’ai fait des tests indentiques au paragraphe précédent (6.3) sur 3 servomoteurs DRS-0101 différents, pour un temps de mouvement de 2 secondes. J’obtiens la figure ci-dessous qui confirme la reproductibilité des résultats – dans une moindre mesure étant donné le faible nombre d’échantillons – à une exception près : le servomoteur 2 décroche plus tôt (à 0,7 N.m alors que les autres décrochent à 0,8 N.m) et le couple qu’il développe à la monté pour une charge de 0,6 N.m est significativement plus élevé que pour les 2 autres. Il s’agit en fait du servomoteur dont j’ai cassé les engrenages lors de précédents tests (voir anectode en conclusion). Lorsque j’ai changé ses engrenages je ne les ai pas regraissés (je n’avais pas de graisse 🙁 ). C’est probablement pour cela que le frottement des engrenages est plus important pour celui-ci.
J’ai montré dans l’article suivant qu’il s’agit en effet d’un problème de graissage et que le résultat est reproductible sur le servomoteur 2 une fois l’engrenage graissé.
6.4 Estimation de la charge
Mon intension initiale était d’être capable d’estimer le couple de charge, mais au vu de la complexité des équations en jeu, je ne crois pas que cela soit faisable sans simplifications importantes du problème. En effet, 3 paramètres sont interdépendants dans l’équation dynamique (Cc, Cf et JO), dont Cf est une fonction non linéaire et discontinue et JO demande de connaitre la répartition de la charge. Et quand bien même on trouverait une solution théorique, je pense que son implémentation génèrerait des résultats peu pertinents du fait des approximations, des micro-régulations du système et de la dispersion des résultats. Je m’arrête donc là pour cette fois.
7 Conclusion
Cette étude m’a permis de me clarifier les idées quand au sens de cette grandeur PWM, et aussi ce que je pouvais espérer en tirer (j’espère que pour vous aussi 🙂 ). Pour résumer, j’ai proposé une modélisation du servomoteur ainsi qu’une hypothèse sur la valeur PWM que j’ai ensuite toutes les deux validées expérimentalement avec des essais en charge statique et en rotation à vide. J’ai ensuite utilisé les données expérimentales pour évaluer les constantes du servomoteur, dont j’ai validé les valeurs par des essais en charges mobiles (à vitesse constante).
Vous pouvez télécharger le fichier libre office calc contenant mes résultats expérimentaux.
Pour terminer je voulais vous mentionner, si vous êtes tenté de faire des essais de charge de ce type, de faire attention à la casse. Lorsque j’avais fait mes premiers tests, j’ai appliqué des couples (en statique) nettement suppérieurs à 1,2 N.m (couple de démarrage nominal) – jusqu’à 2 N.m. Il se trouve que le servomoteur le supportait jusqu’au moment où son engrenage s’est cassé. Heureusement qu’il est possible d’acheter un kit de secours (jeu d’engrenages) à moindre prix et qu’ils sont faciles à changer ! Appliquer une limite PWM max peut éviter ces situations. Comme nous venons de voir, cette valeur va dépendre de la vitesse et du couple, c’est-à-dire qu’en mouvement le couple maximum admissible sera plus faible qu’à l’arrêt.
















Merci pour les informations concernant le signa PWM. Il serait intéressant de montrer l’allure du signal PWM et son effet par exemple sur la vitesse d’un moteur à CC.
Bonjour,
Merci pour votre commentaire. Je ne suis pas sûr de comprendre votre question.
Le signal PWM est un signal en créneaux bien documenté sur internet, entre autre sur le lien que vous fournissez.
Comme expliqué au paragraphe 2/ Hyphothèse : Ua PWM/1023 = K Ω + Cm Ri/K. Si on a aucun couple de résistance, et donc qu’on est en régime constant, la vitesse est proportionnelle à la tension.
Merci, c’est plus complet.