Cet article fait suite à la modélisation décrite précédemment.
Scilab est utilisé dans sa version 5.5.2.
Je vais présenter dans cet article l’implémentation dans Scilab (logiciel de calculs numérique) de la modélisation de la patte, ainsi que des résultats numériques obtenus afin de dimensionner notre patte.
1 Implémentation
L’implémentation dans Scilab des modèles cinématiques direct et inverse, ainsi que le modèle mécanique est réalisée sous forme de fonctions présentée ci-dessous.
1.1 Modèle cinématique direct
// Please refere to http://benoitpuel.com/blog/2016/01/20/geckrobot-concept-et-modelisation-dune-patte/ // Inputs // X0, Y0, Z0: cartesian coordinates of the the foot reference-point (O1) in the robot coordinate system (in millimetre) // Y1, Y2, Y3: foot geometrie, respectively O1->O2, O2->03, and O3->O4 (in millimetre) // theta1, theta2, theta3: angles of the servomotors (in radian) // Outputs // X, Y, Z: cartesian coordinates of the the foot end-point (O4) (in millimetre) function [X, Y, Z] = kinematics_direct_model(X0, Y0, Z0, Y1, Y2, Y3, theta1, theta2, theta3) // pre-processing deltaY = Y1 + Y2 * cos(theta2) + Y3 * cos(theta2 + theta3); deltaZ = Y2 * sin(theta2) + Y3 * sin(theta2 + theta3); // processing X = X0 - deltaY * sin(theta1); Y = Y0 + deltaY * cos(theta1); Z = Z0 + deltaZ; endfunction
1.2 Modèle cinématique inverse
// Please refere to http://benoitpuel.com/blog/2016/01/20/geckrobot-concept-et-modelisation-dune-patte/
// Inputs
// X0, Y0, Z0: cartesian coordinates of the the foot reference-point (O1) in the robot coordinate system (in millimetre)
// Y1, Y2, Y3: foot geometrie, respectively O1->O2, O2->03, and O3->O4 (in millimetre)
// X, Y, Z: cartesian coordinates of the the foot end-point (O4) (in millimetre)
// Outputs
// theta1, theta2, theta3: angles of the servomotors (in radian)
// err: 1 if there is no possible solution, 0 otherwise
function [theta1, theta2, theta3, err] = kinematics_inverse_model(X0, Y0, Z0, Y1, Y2, Y3, X, Y, Z)
// initialization if error occures
theta1 = 0;
theta2 = 0;
theta3 = 0;
err = 1;
// pre-processing
if or([Y2 == 0, Y3 == 0]) then
return;
end
A = sqrt((X - X0)^2 + (Y - Y0)^2);
cosTheta3 = ((A-Y1)^2 + (Z-Z0)^2 - Y2^2 - Y3^2) / (2 * Y2 * Y3);
if abs(cosTheta3) > 1 then
return;
end
theta3tmp = - acos(cosTheta3);
if abs(theta3tmp) < 0.002 then
theta2tmp = atan(Z - Z0, A - Y1);
else
tmp1 = Y2 + Y3*cosTheta3;
tmp2 = Y3*sin(theta3tmp);
cosTheta2 = (tmp1 * (A - Y1) + tmp2 * (Z - Z0)) / (tmp1^2 + tmp2^2);
sinTheta2 = (tmp1 * cosTheta2 - A + Y1) / tmp2;
theta2tmp = atan(sinTheta2, cosTheta2);
end
// processing
theta1 = atan(X0 - X, Y - Y0);
theta2 = theta2tmp;
theta3 = theta3tmp;
err = 0;
endfunction
1.3 Modèle mécanique
// Please refere to http://benoitpuel.com/blog/2016/01/20/geckrobot-concept-et-modelisation-dune-patte/ // Inputs // X0, Y0, Z0: cartesian coordinates of the the foot reference-point (O1) in the robot coordinate system (in millimetre) // Y1, Y2, Y3: foot geometrie, respectively O1->O2, O2->03, and O3->O4 (in millimetre) // theta1, theta2, theta3: angles of the servomotors (in radian) // Fx, Fy, Fz: force applied at the foot end-point (O4) in the robot coordinate system (in newton) // Outputs // C1, C2, C3: torques of the servomotors (in Nm - newton*meter) function [C1, C2, C3] = mechanics_direct_model(X0, Y0, Z0, Y1, Y2, Y3, theta1, theta2, theta3, Fx, Fy, Fz) // pre-processing cosTheta1 = cos(theta1); sinTheta1 = sin(theta1); cosTheta2 = cos(theta2); sinTheta2 = sin(theta2); cosTheta23 = cos(theta2 + theta3); sinTheta23 = sin(theta2 + theta3); tmp1 = Fx*sinTheta1 - Fy*cosTheta1; C3tmp = Y3 * (tmp1*sinTheta23 + Fz*cosTheta23); // processing C1 = - (Y1 + Y2*cosTheta2 + Y3*cosTheta23)*(Fx*cosTheta1 + Fy*sinTheta1); C2 = Y2 * (tmp1*sinTheta2 + Fz*cosTheta2) + C3tmp; C3 = C3tmp; endfunction
1.4 Exemple
Testons d’abord le modèle cinématique direct pour :
- X0 = 0 mm, Y0 = 0 mm, Z0 = 100 mm
- Y1 = 30 mm, Y2 = 50 mm, Y3 = 80 mm
- θ1 = 0°, θ2 = 0°, θ3 = -90°
-->exec('.../kinematics_direct_model.sci',-1);
-->[X, Y, Z] = kinematics_direct_model(0, 0, 100, 30, 50, 80, 0, 0, -%pi/2)
Z =
20.
Y =
80.
X =
0.
Vérifions que le modèle cinématique inverse redonne les mêmes valeurs de θ1, θ2 et θ3.
-->exec('.../kinematics_inverse_model.sci',-1);
-->[theta1, theta2, theta3, err] = kinematics_inverse_model(0, 0, 100, 30, 50, 80, 0, 80, 20)
err =
0.
theta3 =
- 1.5707963
theta2 =
0.
theta1 =
0.
Testons que dans un cas pour lequel il n’existe pas de solution (position trop éloignée pour la patte), la fonction retourne bien err = 1.
-->[theta1, theta2, theta3, err] = kinematics_inverse_model(0, 0, 100, 30, 50, 80, 0, 200, 0)
err =
1.
theta3 =
0.
theta2 =
0.
theta1 =
0.
Testons aussi que le cas où θ3 = 0 est bien pris en compte.
-->[theta1, theta2, theta3, err] = kinematics_inverse_model(0, 0, 100, 30, 50, 80, 0, 160, 100)
err =
0.
theta3 =
0.
theta2 =
0.
theta1 =
0.
Finalement, testons le modèle mécanique pour la même configuration, en considérant l’effort suivant :
- Fx = 10 N, Fy = 20 N, Fz = 100 N (qu’on exprime aussi parfois abusivement 1 kg, 2 kg et 10 kg respectivement)
-->exec('.../mechanics_direct_model.sci',-1)
-->[C1, C2, C3] = mechanics_direct_model(0, 0, 100, 30, 50, 80, 0, 0, -%pi/2, 10, 20, 100)
C3 =
1600.
C2 =
6600.
C1 =
- 800.
Ces résultats (grandeurs et signes) sont cohérents avec une approche “avec les doigts”.
2 Dimensionnement
Le dimensionnement consiste à définir les valeurs de nos constantes de calcul (X0, Y0, Z0, Y1, Y2 et Y3) ainsi que les couples (C1, C2 et C3) que doivent fournir les servomoteurs.
2.1 Cahier des charges
J’ai défini le cahier des charges suivant :
- La course de la patte est de 100 mm sur l’axe x.
- La course de la patte est de 50 mm sur l’axe y.
- Le robot doit pouvoir évoluer sur une surface courbe, dont le rayon de courbure (qu’on écrira Rc) peut descendre à 200 mm (concave ou convexe).
- Le robot pourra peser jusqu’à 7,5 kg, soit une charge de 1,5 kg par patte lorsqu’une des 6 pattes est levée.
2.2 Zone de travail
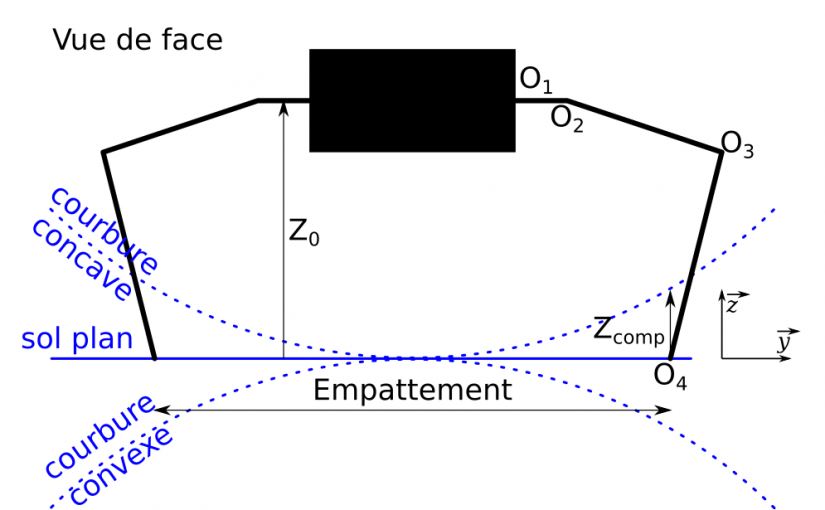
Ce pré-dimensionnement consiste à traduire la problématique depuis un rayon de courbure vers une course suivant l’axe z. Pour cela commençons par schématiser le problème.
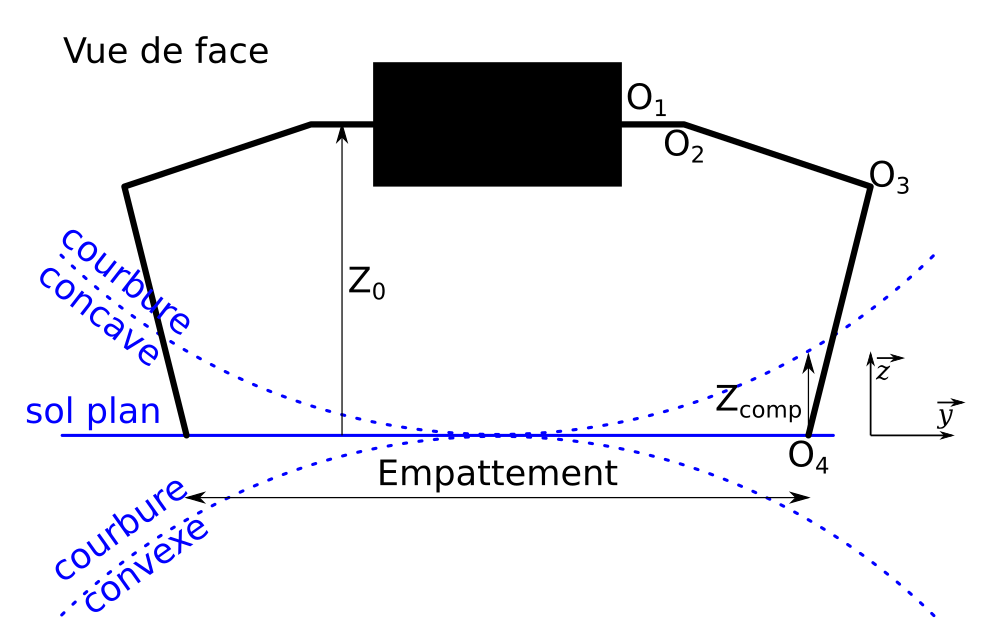Je commence par faire l’hypothèse de départ, d’un empattement maximum (qu’on écrira emp) – écart maximum entre deux pattes en vis-à-vis – de 200 mm. Le schéma ci-dessus nous montre que la position des pattes doit être compensée en hauteur (qu’on écrira Zcomp) lorsque la surface est courbée. Nous considérons la courbure constante sur la largeur de l’empattement.
Une simple application du théorème de Pythagore nous donne
Zcomp = Rc – √(Rc2 – (emp/2)2) = 26,8 mm.
Je vais arrondir pour la suite sa valeur à Zcomp = 30 mm. Nous pouvons maintenant définir la zone de travail – zone de l’espace dans laquelle une patte doit pouvoir travailler :
- X ∈ [X0 – 50 mm, X0 + 50 mm] : course de 100 mm suivant x, centrée autour de X0 ;
- Y ∈ [Y0, Y0 + 50 mm] : course de 50 mm suivant y, démarrant à partir de Y0 ;
- Z ∈ [- 30 mm, 50 mm] : compensation sur z de ± 30 mm autour de la référence de l’axe z du robot, et un jeu de 20 mm supplémentaire pour permettre de “lever la patte” sans toucher le sol.
2.3 Étude paramétrique
Nous allons traiter le problème par le biais d’une étude paramétrique, nous allons donc tester un grand nombre de solutions en faisant varier la valeur des paramètres Z0, Y1, Y2 et Y3. Les paramètres X0 et Y0 n’influant pas sur les performances, ils seront définis pour l’étude : X0 = Y0 = 0. Leurs valeurs seront définies pour chaque patte individuellement lorsque nous nous intéresserons à la conception du robot dans son ensemble.
Nous allons mener cette étude de façon “brute”, nous évaluerons toutes les solutions afin que chaque paramètre soit étudiés avec un pas de 5 mm dans l’espace de recherche suivant :
- Z0 ∈ [60 mm, 200 mm] : 60 mm est le minimum pour que les pièces mécaniques soient au dessus de la zone de travail, 200 mm permet de limiter la hauteur du robot ;
- Y1 ∈ [30 mm, 80 mm] : 30 mm est le minimum pour l’entre-axe entre deux servomoteurs perpendiculaires, 80 mm permet de limiter la largeur du robot ;
- Y2 ∈ [40 mm, 200 mm] : 40 mm est le minimum pour l’entre-axe entre deux servomoteurs parallèles, 200 mm permet de limiter l’encombrement du robot ;
- Y3 ∈ [80 mm, 200 mm] : 80 mm est le minimum pour loger un système de ventouse en bout de patte, 200 mm permet de limiter l’encombrement du robot.
2.4 Problème contraint
Le problème ainsi posé demande d’évaluer 263175 solutions, dites solutions candidates. Nous avons vu dans le modélisation (section 3) qu’en fonction des valeurs de Z0, Y1, Y2 et Y3 il est possible ou non d’atteindre une coordonnée X, Y, Z. Dans le code proposé au paragraphe 1.2 de cet article, la variable de sortie err renseigne lorsque ce cas de figure se présente. Nous allons donc tester les solutions candidates et ne retenir que celles qui permettent d’atteindre tous les points de l’espace de travail, exploré avec un pas de 10 mm sur chacun des axes.
La routine suivante permet de déterminer toutes les solutions dites faisables, c’est à dire qui permettent d’explorer entièrement l’espace de travail.
// Inputs
// X0range, Y0range, Z0range: parameter ranges for cartesian coordinates of the the foot reference-point O1 in the robot coordinate system (in millimetre)
// Y1range, Y2range, Y3range: parameter ranges for foot geometrie, respectively O1->O2, O2->03, and O3->O4 (in millimetre)
// Xrange, Yrange, Zrange: variable ranges test for cartesian coordinates of the foot end-point O4 (in millimetre)
// Outputs
// feasibleSolutions: all the feasable solutions with the format feasibleSolutions(i,:) = [X0, Y0, Z0, Y1, Y2, Y3]
function feasibleSolutions = constrained_problem(X0range, Y0range, Z0range, Y1range, Y2range, Y3range, Xrange, Yrange, Zrange)
// load function in case it is not already done
exec('./kinematics_inverse_model.sci',-1);
// count of solutions
nb_sol = 0;
nb_tot_eval = size(X0range,2)*size(Y0range,2)*size(Z0range,2)*size(Y1range,2)*size(Y2range,2)*size(Y3range,2);
nb_eval = 0;
// start the processing evolution display
tic();
mprintf('processing : %i pourcent \n',0);
mprintf('processing : %ih %imin %isec \n \n',0, 0, 0);
// loop on all variables to scan the domain
for X0 = X0range
for Y0 = Y0range
for Z0 = Z0range
for Y1 = Y1range
for Y2 = Y2range
for Y3 = Y3range
isError = 0;
for X = Xrange
for Y = Yrange
for Z = Zrange
[theta1, theta2, theta3, err] = kinematics_inverse_model(X0, Y0, Z0, Y1, Y2, Y3, X, Y, Z);
if err == 1 then
isError=1;
break;
end;
end;
if isError==1 then
break;
end;
end;
if isError==1 then
break;
end;
end;
if isError == 0 then
nb_sol = nb_sol + 1;
feasibleSolutions(nb_sol,:) = [X0, Y0, Z0, Y1, Y2, Y3];
end;
nb_eval = nb_eval + 1;
end;
end;
// update the processing evolution display
clc(1);
pourcent = round(nb_eval * 100 / nb_tot_eval);
mprintf('processing : %i pourcent \n',pourcent);
time = toc(); hour = floor(time/3600); minute = floor(modulo(time,3600)/60); second = modulo(time,60);
mprintf('processing : %ih %imin %isec \n \n',hour, minute, second);
end;
end;
end
end
// display the number of feasible solutions
mprintf('feasible solutions : %i \n',nb_sol);
endfunction
Nous obtenons 157707 solutions faisables sur les 263175 solutions candidates, soit 60%.
-->exec('.../contrained_problem.sce',-1)
-->feasibleSolutions = constrained_problem(0, 0, 60:5:200, 30:5:80, 40:5:200, 80:5:200, -50:10:50, 0:10:50, -30:10:50);
processing : 100 pourcent
processing : 1h 0min 42sec
feasible solutions : 157707
2.5 Evaluation des solutions
Nous avons retiré toutes les solutions qui ne répondent pas au problème. Nous devons maintenant identifier un/des critère(s) de choix, appelés objectifs (ou fonction coût), pour retenir la meilleur d’entre elles. J’ai listé les objectifs suivants :
- Minimiser le couple appliqué aux servomoteurs, car cela permet de réduire leur coût et leur encombrement.
- Minimiser la plage angulaire de l’orientation du bout de la patte (donnée par θ2+θ3). En effet, la ventouse devra avoir 3 degrés de liberté en rotation afin de pouvoir garantir un contact correct sur la surface, d’autant plus lorsque celle-ci est courbée. En minimisant ces variations d’angles, nous réduisons alors les débattement angulaires nécessaires, et donc facilitons la future conception mécanique de cette rotule.
Les solutions faisables sont évaluées avec ces objectifs par la routine suivante.
// Inputs
// feasibleSolutions: all the feasable solutions with the format feasibleSolutions(i,:) = [X0, Y0, Z0, Y1, Y2, Y3]
// Xrange, Yrange, Zrange: variable ranges test for cartesian coordinates of the foot end-point O4 (in millimetre)
// Fx, Fy, Fz: force applied at the foot end-point (O4) in the robot coordinate system (in newton)
// Outputs
// evaluatedSolutions: all the evaluated solutions with the format evaluatedSolutions(i,:) = [X0, Y0, Z0, Y1, Y2, Y3, minTheta1, minTheta2, minTheta3, minTheta2+3, maxTheta1, maxTheta2, maxTheta3, maxTheta2+3, maxC1, maxC2, maxC3]
function evaluatedSolutions = evaluation(feasibleSolutions, Xrange, Yrange, Zrange, Fx, Fy, Fz)
// load function in case it is not already done
exec('./kinematics_inverse_model.sci',-1);
exec('./mechanics_direct_model.sci',-1);
// count of solutions
nb_tot_eval = size(feasibleSolutions,1);
// start the processing evolution display
tic();
mprintf('processing : %i pourcent \n',0); pourcent = 0;
mprintf('processing : %ih %imin %isec \n \n',0, 0, 0);
// loop on all variables to scan the domain
for i = 1:nb_tot_eval
minThetas = 2*%pi*ones(1,4);
maxThetas = -2*%pi*ones(1,4);
maxCs = zeros(1,3);
for X = Xrange
for Y = Yrange
for Z = Zrange
[theta1, theta2, theta3, err] = kinematics_inverse_model(feasibleSolutions(i,1), feasibleSolutions(i,2), feasibleSolutions(i,3), feasibleSolutions(i,4), feasibleSolutions(i,5), feasibleSolutions(i,6), X, Y, Z);
minThetas = min(minThetas, [theta1, theta2, theta3, theta2+theta3]);
maxThetas = max(maxThetas, [theta1, theta2, theta3, theta2+theta3]);
[C1x, C2x, C3x] = mechanics_direct_model(feasibleSolutions(i,1), feasibleSolutions(i,2), feasibleSolutions(i,3), feasibleSolutions(i,4), feasibleSolutions(i,5), feasibleSolutions(i,6), theta1, theta2, theta3, Fx, 0, 0);
[C1y, C2y, C3y] = mechanics_direct_model(feasibleSolutions(i,1), feasibleSolutions(i,2), feasibleSolutions(i,3), feasibleSolutions(i,4), feasibleSolutions(i,5), feasibleSolutions(i,6), theta1, theta2, theta3, 0, Fy, 0);
[C1z, C2z, C3z] = mechanics_direct_model(feasibleSolutions(i,1), feasibleSolutions(i,2), feasibleSolutions(i,3), feasibleSolutions(i,4), feasibleSolutions(i,5), feasibleSolutions(i,6), theta1, theta2, theta3, 0, 0, Fz);
maxCs = max(maxCs, abs([C1x, C2x, C3x]), abs([C1y, C2y, C3y]), abs([C1z, C2z, C3z]));
end;
end;
end;
evaluatedSolutions(i,:) = [feasibleSolutions(i,1:6), minThetas(1:4), maxThetas(1:4), maxCs(1:3)];
// update the processing evolution display
if floor(i * 100 / nb_tot_eval) > pourcent then
clc(1);
pourcent = floor(i * 100 / nb_tot_eval);
mprintf('processing : %i pourcent \n',pourcent);
time = toc(); hour = floor(time/3600); minute = floor(modulo(time,3600)/60); second = modulo(time,60);
mprintf('processing : %ih %imin %isec \n \n',hour, minute, second);
end
end
endfunction
Cette fois-ci l’évaluation ne se fait pas sur tout l’espace de travail, mais seulement sur la zone dans laquelle la patte peut être en contact avec le sol. En effet, lorsqu’on soulève la patte, aucun couple (autre que celui dû à son propre poids) n’est appliqué et la ventouse n’a pas besoin de s’adapter à une position particuliaire. Aussi, les calculs sont réalisés pour une force de 15 N (soit 1,5 kg) en bout de patte (en O4). Cette force est appliquée séparément sur chaque axe (x, y et z) pour simuler respectivement les situations suivantes :
- robot vertical sur un mur
- robot horizontal sur un mur
- robot au plafond
-->exec('.../evaluation.sce',-1)
-->evaluatedSolutions = evaluation(feasibleSolutions, -50:10:50, 0:10:50, -30:10:30, 15, 15);
processing : 100 pourcent
processing : 2h 58min 34sec
La liste des solutions évaluée est donnée dans le fichier libre office calc.
2.6 Choix d’une solution
Pour faire un choix parmis toutes ces solutions, nous allons procéder méthodiquement en observant les résultats obtenus suite à l’évaluation.
Remarquez que le couple maximum C1 est identique pour toutes les solutions (750 N.mm soit 7,5 kg.cm). Ce résultat se retrouve dans la modélisation, en assemblant plusieurs équations (en passant par la variable intermédiaire A) on trouve que C1 ne dépend que de l’espace de travail. Nous observons aussi que la valeur de C2 est directement proportionnelle à la valeur de Z0, ce qui peut aussi se retrouver dans les équations, lorsqu’une force Fy est appliquée. La valeur de C2 varie de 1350 N.mm (soit 13,5 kg.cm) à 3450 N.mm (soit 34,5 kg.cm). La valeur de C3 ne présente pas de corrélation simple avec les paramètres, et sa valeur varie de 1152 N.mm (soit 11,5 kg.cm) à 3000 N.mm (soit 30 kg.cm).
Les servomoteurs avec lesquels j’ai commencé à travailler sont les HerkuleX DRS-0101 dont le couple de démarrage est de 12 kg.cm. Si cette valeur est suffisante pour C1, elle est insuffisante pour C2 et juste suffisante pour quelques cas pour C3. Heureusement son grand frère le DRS-0201 a le même design, se pilote de la même manière et propose un couple de démarrage de 24 kg.cm ; la contrepartie étant qu’il passe de 30€ à 100€ l’unité…
J’ai donc écrit la routine suivante qui, en fonction de critères de couples maximum pour C2 et C3, retourne la solution donnant la plus petite plage angulaire de l’orientation du bout de la patte.
// Inputs
// evaluatedSolutions: all the evaluated solutions with the format evaluatedSolutions(i,:) = [X0, Y0, Z0, Y1, Y2, Y3, minTheta1, minTheta2, minTheta3, minTheta2+3, maxTheta1, maxTheta2, maxTheta3, maxTheta2+3, maxC1, maxC2, maxC3]
// Outputs
// optimSolution: optimal solutions with the format paretoSolutions(1,:) = [X0, Y0, Z0, Y1, Y2, Y3, minTheta1, minTheta2, minTheta3, minTheta2+3, maxTheta1, maxTheta2, maxTheta3, maxTheta2+3, maxC1, maxC2, maxC3]
function optimSolution = selection(evaluatedSolutions, maxC2, maxC3)
nbSol = size(evaluatedSolutions,1);
optim_sol = 0;
for i = 1:1:nbSol
// do not consider high torques
if evaluatedSolutions(i,16) > maxC2 | evaluatedSolutions(i,17) > maxC3 then
continue;
end
if optim_sol == 0 then // 1st solution is optim
optim_sol = i;
else
if (evaluatedSolutions(i,14)-evaluatedSolutions(i,10)) < (evaluatedSolutions(optim_sol,14)-evaluatedSolutions(optim_sol,10)) then
optim_sol = i;
end
end
end
optimSolution = evaluatedSolutions(optim_sol,:);
endfunction
Voici les résultats pour les 2 cas de figure :
- C2 → DRS-0201 et C3 → DRS-0101 (optimSolution1)
| Z0 (mm) | Y1 (mm) | Y2 (mm) | Y3 (mm) | Plage ang. (deg) | C1 (N.mm) | C2 (N.mm) | C3 (N.mm) |
| 130 | 80 | 120 | 80 | 55 | 750 | 2400 | 1200 |
- C2 → DRS-0201 et C3 → DRS-0201 (optimSolution2)
| Z0 (mm) | Y1 (mm) | Y2 (mm) | Y3 (mm) | Plage ang. (deg) | C1 (N.mm) | C2 (N.mm) | C3 (N.mm) |
| 130 | 75 | 100 | 165 | 37 | 750 | 2400 | 2380 |
-->exec('.../selection.sce',-1);
-->optimSolution1 = selection(evaluatedSolutions, 2400, 1200);
-->optimSolution2 = selection(evaluatedSolutions, 2400, 2400);
Ces solutions sont détaillée dans le fichier libre office calc.
Télécharger tout le code utilisé dans cet article.
3 Conclusion
L’outil numérique nous a permis de traiter un problème pour lequel il n’existe pas de réponse évidente ou calculable directement. Je dois reconnaître qu’en écrivant cet article j’ai du faire preuve de plus de rigueure que lors de mes premiers essais et les résultats que j’obtiens ici sont très différents. La différence vient principalement du fait que je n’avais initialement pensé qu’à prendre en compte le cas du robot “au plafond” et homis celui du robot “sur un mur”.